Công thức tổ hợp, chỉnh hợp, hoán vị và các dạng bài tập có lời giải – Tin Công Nghệ

1️⃣ Công thức tổ hợp, chỉnh hợp, hoán vị và các dạng bài tập có lời giải – Tin Công Nghệ ✔️

1 Hoán vị

Định nghĩa hoán vị

Hoán trong hoán đổi và vị trong vị trí. Có tức là nếu chúng ta có 1 tập hợp n phần tử (n> 0), thì mỗi cách sắp xếp n thành phần đó theo một thứ tự thì ta được một hoán vị của n phần tử đó.

Công thức hoán vị

Để tính hoán vị, ta sử dụng công thức:

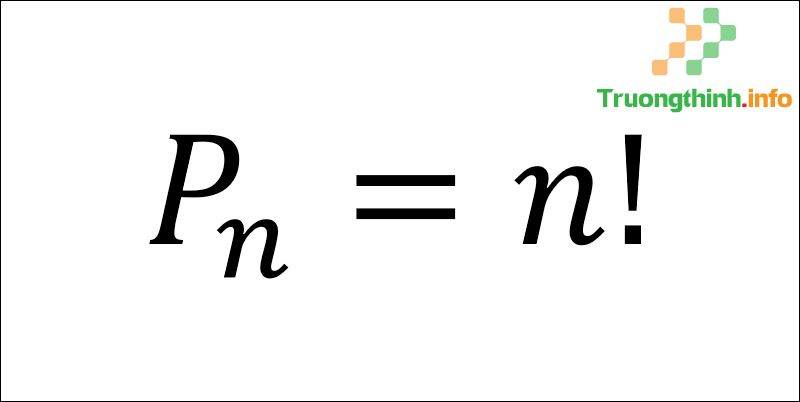
Công thức tính hoán vị

Ví dụ hoán vị

Câu hỏi thí dụ : Cho tập A = {3, 4, 5, ,6, 7}. Từ tập A có thể lập được bao nhiêu số gồm 5 chữ số phân biệt?

Đáp án : 5!= 5 x 4 x 3 x 2 x 1 = 120 số.

Đáp án ví dụ hoán vị

2 Chỉnh hợp

Định nghĩa chỉnh hợp

Cho tập hợp A gồm có n phần tử. Một bộ gồm k ( với 1 nhỏ hơn hoặc bằng k và k nhỏ hơn hoặc bằng n) phần tử sắp thứ tự của tập hợp A được coi là một chỉnh hợp chập k của n thành phần của tập hợp A.

Công thức chỉnh hợp

Để tính chỉnh hợp, ta sử dụng công thức sau:

Công thức để tính chỉnh hợp

Ví dụ chỉnh hợp

Câu hỏi thí dụ : Có bao nhiêu cách xếp ba khách Ngọc, Khánh, Ngân vào hai chỗ ngồi cho trước?

Đáp án :

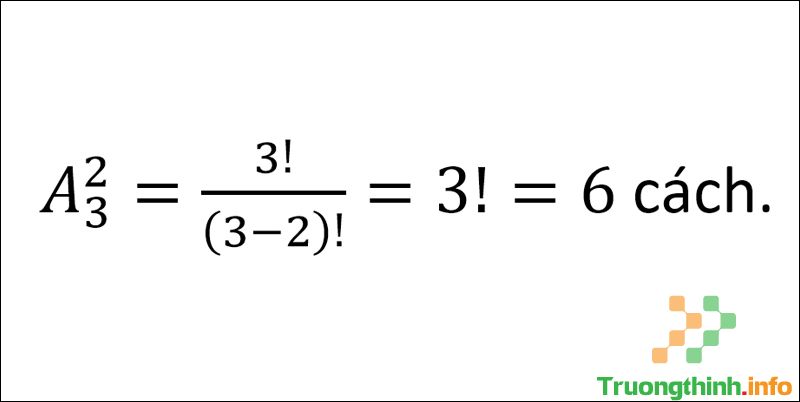
Đáp án cho ví dụ của chỉnh hợp

3. Tổ hợp

Định nghĩa tổ hợp

Cho tập hợp A bao gồm n phần tử. Một tập con của A gồm có k thành phần phân biệt ( với 1 nhỏ hơn hoặc bằng k và k nhỏ hơn hoặc bằng n), được coi là một tổ hợp chập k của n phần tử của A.

Công thức tổ hợp

Dưới đây là các công thức để tính tổ hợp (với k, n hợp lệ):

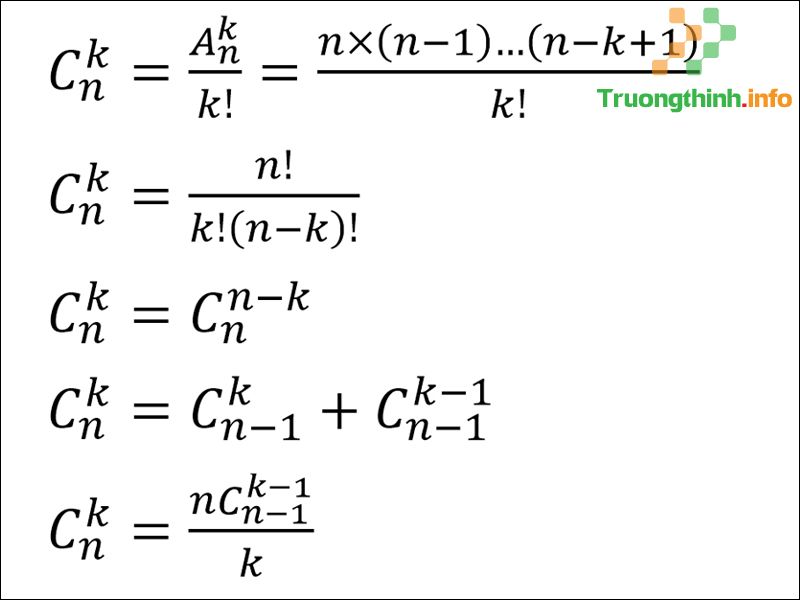
Các công thức tính tổ hợp

Ví dụ tổ hợp

Câu hỏi ví dụ : Ông X có 11 người bạn. Ông ta muốn mời 5 người trong số họ đi chơi xa. Trong 11 người đó có 2 người không muốn họp mặt nhau. Hỏi ông X có bao nhiêu cách mời?

Đáp án :

Đáp án là 378 cách

4. Công thức nhị thức Newton

Dưới này là công thức nhị thức Newton:

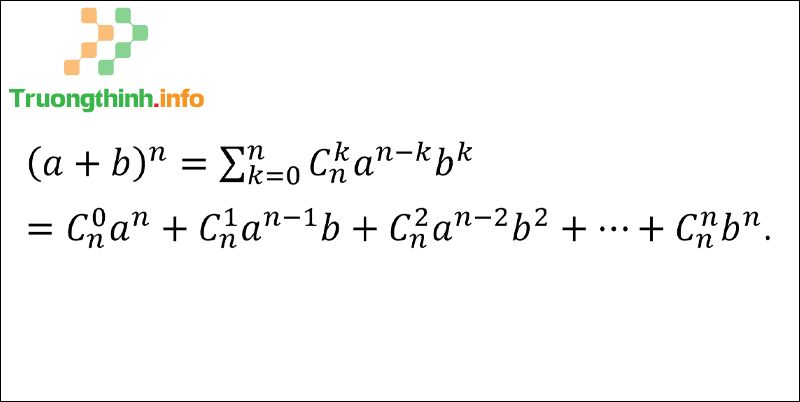
Công thức nhị thức Newton

5. Tổng hợp các công thức quan trọng của tổ hợp, chỉnh hợp, hoán vị

Dưới này là tổng hợp các công thức quan trọng của tổ hợp, chỉnh hợp và hoán vị:

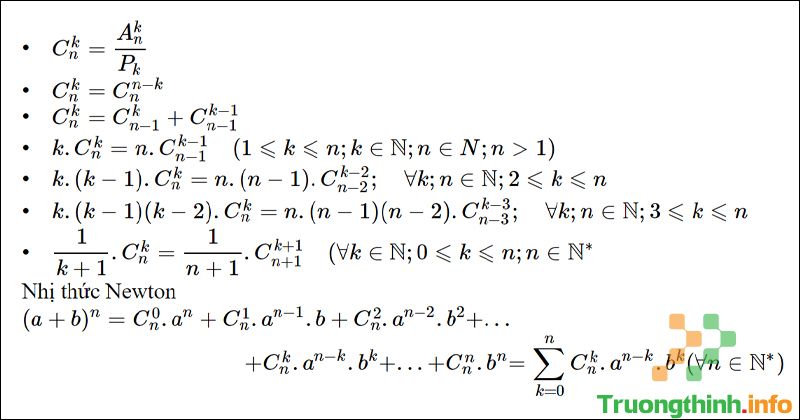
Các công thức quan trọng

6. Phân biệt tổ hợp, chỉnh hợp và hoán vị

Bảng dưới đây sẽ giúp bạn phân biệt được tổ hợp, chỉnh hợp và hoán vị:

Bảng phân biệt

7. Phương pháp giải phương trình, bất phương trình, hệ phương trình tổ hợp

Phương pháp giải phương trình, bất phương trình và hệ phương trình tổ hợp không vượt quá khó, chỉ cần bạn lần lượt thực hành các bước dưới đây:

+ Bước 1 : Đặt điều kiện có nghĩa: Các chỉ số phải là số tự nhiên và chữ số dưới phải lớn hơn hoặc bằng chỉ số trên.

+ Bước 2 : Sử dụng các công thức của hoán vị, chỉnh hợp và tổ hợp.

+ Bước 3 : Biến đổi phương trình, bất phương trình cho đơn giản rồi bắt đầu tìm nghiệm.

+ Bước 4 : Đối chiếu kết quả với điều kiện rồi kết luận.

Phương pháp giải phương trình, bất phương trình và hệ phương trình tổ hợp

8. Các dạng bài tập toán về hoán vị, chỉnh hợp và tổ hợp

Dạng 1: Bài toán đếm

– Để nhận dạng một bài toán đếm có sử dụng hoán vị của n phần tử, chúng ta sẽ dựa theo những dấu hiệu sau:

+ Tất cả n thành phần đều có mặt.

+ Mỗi phần tử chỉ xuất hiện 1 lần.

+ Có phân biệt thứ tự giữa các phần tử.

– Nhận dạng một bài toán đếm có sử dụng chỉnh hợp chập k của n phần tử, ta sẽ dựa theo một số triệu chứng sau:

+ Phải chọn k thành phần từ n thành phần cho trước.

+ Có phân biệt thứ tự giữa k phần tử được chọn.

Các dạng bài tập

– Bài toán đếm có sử dụng tổ hợp chập k của n phần tử sẽ có nhận ra qua các dấu hiệu sau:

+ Phải chọn k phần tử từ n thành phần cho trước.

+ Không phân biệt thứ tự giữa k phần tử được chọn.

Dạng 2: Rút gọn và tính giá trị biểu thức

Để rút gọn các biểu thức chứa hoán vị, chỉnh hợp, tổ hợp ta biến đổi linh hoạt dựa theo các công thức để tiếp về dạng dễ dàng dần.

Dạng 3: Chứng minh đẳng thức, bất đẳng thức

Để chứng minh đẳng thức, bất đẳng thức ta sử dụng các công thức của tổ hợp. Người ta thường sử dụng các cách sau:

+ Cách 1 : Dùng các phép biến đổi.

+ Cách 2 : Đánh giá vế của bất đẳng thức.

+ Cách 3 : Chứng minh quy nạp.

+ Cách 4 : Dùng phương pháp đếm.

Dạng bài tập minh chứng đẳng thức và bất đẳng thức

Dạng 4: Giải phương trình, hệ phương trình

Để giải dạng bài toán phương trình, hệ phương trình người ta thường sử dụng 1 trong 2 cách dưới đây:

+ Cách 1 : Thực hiện việc dễ dàng biểu thức hoán vị, chỉnh hợp và tổ hợp để chuyển phương trình về dạng đại số quen thuộc.

+ Cách 2 : Đánh giá thông qua giá trị cận trên hoặc cận dưới.

9. Bài tập về hoán vị, tổ hợp, chỉnh hợp có đáp án

Bài tập trắc nghiệm

Câu 1 : Có bao nhiêu khả năng cũng có thể có thể diễn ra đối với thứ tự giữa các đội trong 1 giải bóng có 5 đội bóng? (giả sử rằng không có hai đội nào có điểm trùng nhau)

A. 120.

B. 100.

C. 80.

D. 60.

Đáp án : A.

Số các khả năng có thể xảy ra đối với thứ tự giữa các đội trong một giải bóng có 5 đội bóng là một hoán vị của 5 thành phần nên có 5! = 120 cách.

Câu 2 : Có bao nhiêu cách xếp không trùng lặp cho 5 người đang ngồi vào 1 bàn dài?

A. 120.

B. 5.

C. 20.

D. 25.

Đáp án : A.

Số cách bố trí khác nhau cho 5 người ngồi xuống 1 bàn dài là một hoán vị của 5 thành phần nên có 5! = 120 cách.

Câu 3 : Giả sử có bảy bông hoa không trùng lặp và ba lọ hoa khác nhau. Hỏi có bao nhiêu cách cắm ba bông hoa vào ba lọ đã cho (mỗi lọ cắm một bông)?

A. 35.

B. 30240.

C. 210.

D. 21.

Đáp án : C.

Số cách xếp bảy bông hoa khác nhau vào ba lọ hoa không trùng lặp là một chỉnh hợp chập 3 của 7 phần tử, suy ra có 210 cách.

Câu 4 : Có 4 nữ sinh tên là Huệ, Hồng, Lan, Hương và 4 nam sinh tên là An, Bình, Hùng, Dũng cùng ngồi quanh 1 bàn tròn có 8 chỗ ngồi. Hỏi có bao nhiêu cách bố trí biết nữ và nam ngồi đan xen nhau?

A. 576.

B. 144.

C. 2880.

D. 1152.

Đáp án : B.

Giả sử các ghế ngồi đánh số từ 1 đến 8.

Chọn 1 bạn bất kì ngồi vô 1 vị trí tình cờ trên bàn tròn có 1 cách. (Nếu chọn 8 cách thì nghĩa là nhầm với bàn dài).

Xếp 3 bạn cùng giới tính còn lại vào 3 ghế (có số ghế cùng tính chẵn hoặc lẻ với bạn đầu) có 3! cách.

Xếp 4 bạn còn lại ngồi xen kẽ 4 bạn đã xếp phía trên có 4! cách.

Vậy có 3! x 4! = 144 cách.

Câu 5 : Có bao nhiêu cách sắp xếp 4 người vào 4 ghế ngồi được sắp xếp quanh một bàn tròn?

A. 12.

B. 24.

C. 4.

D. 6.

Đáp án : D.

Chọn 1 người đang ngồi vào 1 vị trí bất kì . Xếp 3 người còn sót lại vào 3 ghế trống của bàn là một hoán vị của 3 thành phần nên có 3! = 6 cách.

Bài tập tự luận

Câu 1 : Sắp xếp 5 người vào một băng ghế có 5 chỗ. Hỏi có bao nhiêu cách?

Đáp án :

Mỗi cách đổi chỗ 1 trong 5 người trên băng ghế là 1 hoán vị.

Vậy có P = 5! = 120 cách.

Câu 2 : Trong một ban chấp hành đoàn gồm 7 người, cần chọn 3 người trong ban thường vụ. Nếu không có sự phân biệt về chức vụ của 3 người trong ban thường vụ thì có bao nhiêu các chọn?

Đáp án :

Vì không xét đến sự phân biệt chức vụ của 3 người trong ban thường vụ nên mỗi cách chọn ứng với một tổ hợp chập 3 của 7 phần tử. Vì vậy, ta có:

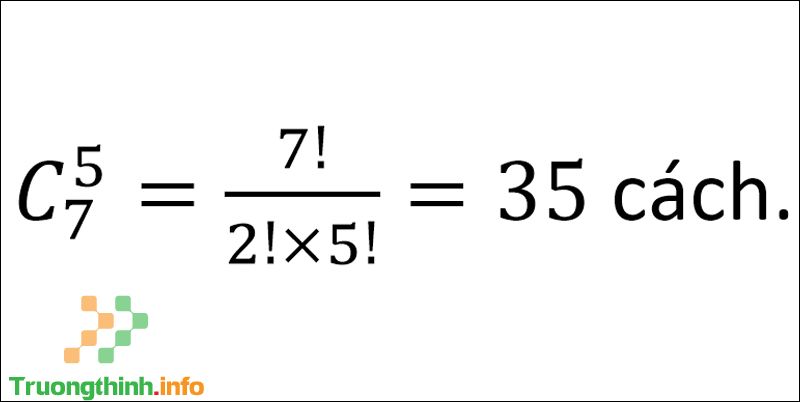
Có 35 cách chọn ban thường vụ

Vậy ta có 35 cách chọn ban thường vụ.

Câu 3 : Trong mặt phẳng có bao nhiêu hình chữ nhật được tạo thành từ bốn đường thẳng phân biệt đi đôi cùng nhau và năm đường thẳng phân biệt vuông góc với bốn đường thẳng đi đôi đó.

Đáp án :

Cứ 2 đường thẳng song song với 2 đường thẳng vuông góc với chúng cắt nhau tại bốn điểm là 4 đỉnh của hình chữ nhật.

Vậy lấy 2 đường thẳng trong 4 đường thẳng song song và lấy 2 đường thẳng trong 5 đường thẳng vuông góc với 4 đường đó ta được số hình chữ nhật là:

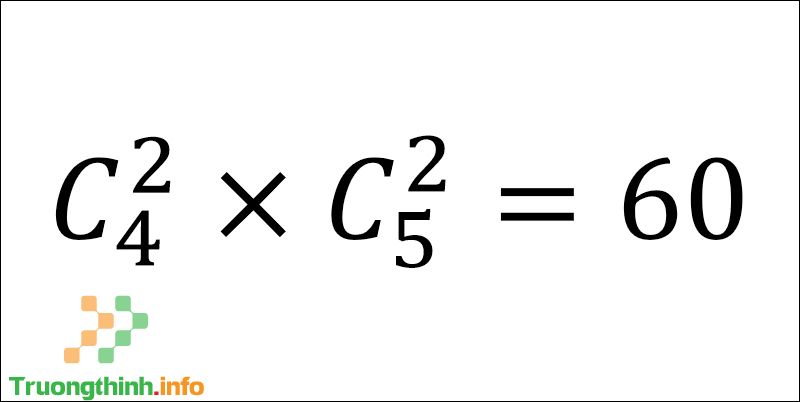
Có 60 hình chữ nhật

Vậy có 60 hình chữ nhật.

10. Cách bấm máy tính cầm tay tính tổ hợp, chỉnh hợp, hoán vị

Cách bấm máy tính cầm tay tính tổ hợp, chỉnh hợp, hoán vị vô cùng đơn giản, chỉ cần thực hiện 1 bước như sau:

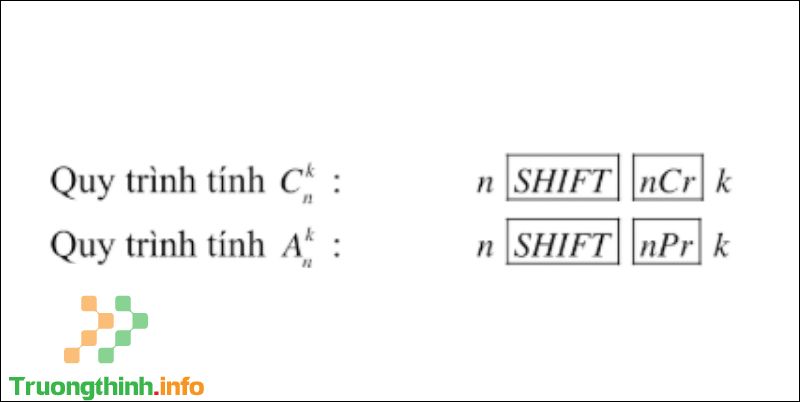
Cách bấm máy tính dễ dàng tính tổ hợp, chỉnh hợp và hoán vị

Tuy nhiên, để giải phương trình hoán vị, tổ hợp và chỉnh hợp thì cách bấm sẽ khó hơn và phải dùng hãng máy tính Casio fx 570 ES trở lên:

Cần sử dụng hãng máy Casio fx 570 ES trở lên để tính phương trình

11. Một số lưu ý về dạng tổ hợp, chỉnh hợp, hoán vị

– Cần đọc kỹ đề bài để không bỏ qua những dữ kiện quan trọng.

– Máy tính cầm tay đích thực rất cần thiết khi làm các bài tập về tổ hợp, chỉnh hợp, hoán vị.

– Biết phân biệt các dạng bài tập.

Một số lưu ý cần phải biết

– Biết phân biệt tổ hợp, chỉnh hợp và hoán vị.

– Thường xuyên làm bài tập để không quên hoặc ghi nhớ sai lệch về kiến thức vì đây là lượng kiến thức quan trọng xuất hiện trong thi cử.

Một số mẫu Máy tính cầm tay Flexio đang buôn bán tại Chúng tôi:

Trên này là bài viết tổng hợp các công thức và bài tập của hoán vị, tổ hợp và chỉnh hợp. Rất mong bài viết sẽ hữu ích với bạn và hẹn gặp lại ở những bài viết sau!

chỉnh hợp,hoán vị,nhị thức newton,tổ hợp,công thức

Nội dung ✔️ Công thức tổ hợp, chỉnh hợp, hoán vị và các dạng bài tập có lời giải – Tin Công Nghệ được tổng hợp sưu tầm biên tập bởi 1️⃣❤️: Trường Thịnh Group. Mọi ý kiến vui lòng gửi Liên Hệ cho truongthinh.info để điều chỉnh. truongthinh.info tks.