Lý thuyết và bài tập tìm hai số khi biết hiệu và tỉ của hai số đó – Tin Công Nghệ

1️⃣ Lý thuyết và bài tập tìm hai số khi biết hiệu và tỉ của hai số đó – Tin Công Nghệ ✔️

1. Bài toán về hiệu tỉ là gì ?

Từ hiệu là kết quả của phép trừ và tỉ là kết quả của phép chia ta cũng có thể có thể kết luận rằng bài toán về hiệu tỉ là cho biết hiệu và tỉ số của hai số và đòi hỏi tìm hai số đó.

2. Cách giải dạng bài tìm hai số khi biết hiệu và tỉ số của hai số đó

Để giải dạng bài toán tìm hai số khi biết hiệu và tỉ số của hai số đó ta thực hiện các bước sau:

+ Bước 1 : Dựa vào tỉ số lập lược đồ đoạn thẳng biểu diễn cho hai số.

+ Bước 2 : Tìm hiệu số phần bằng nhau bằng phương pháp xác định hiệu số phần rồi dựa vào hiệu để tính giá trị 1 phần bằng bao nhiêu đơn vị.

+ Bước 3 : Xác định số bé: Số bé = Hiệu : Hiệu số phần x Số phần của số bé .

+ Bước 4 : Xác định số lớn: Số lớn = Số bé + Hiệu .

Cách giải dạng bài tìm hai số khi biết hiệu và tỉ

3. Các tình huống đặc biệt tìm hai số lúc biết hiệu và tỉ số

Tuy nhiên không phải đề bài nào cũng sẽ cung cấp đủ dữ kiện để chúng ta cũng có thể thực hiện tính toán dễ dàng. Nhiều tình huống đề bài sẽ không cho bạn các dữ kiện đầy đặn về hiệu và tỉ số mà có thể cho những dữ kiện như sau:

+ Trường hợp 1 : Thiếu hiệu (Cho biết tỉ số, không cho biết hiệu số).

+ Trường hợp 2 : Thiếu tỉ (Cho biết hiệu số, không cho thấy tỉ số).

+ Trường hợp 3 : Cho dữ kiện thêm, bớt số, tạo hiệu (tỉ) mới tìm số ban đầu.

Các tình huống đặc biệt

4. Các dạng bài toán tìm hai số khi biết hiệu và tỉ số

Dạng 1: Dạng toán hiệu – tỉ cơ bản

Dạng toán hiệu – tỉ cơ bản là dạng đề cho thấy hiệu, tỉ số sau đó yêu cầu tìm từng thành phần.

Bài tập tỉ dụ : Hiện nay Mẹ hơn Minh 21 tuổi, biết tuổi Mẹ bằng 5/2 tuổi của Minh. Tính tuổi của Mẹ và Minh.

Cách giải :

+ Vẽ sơ đồ bài toán.

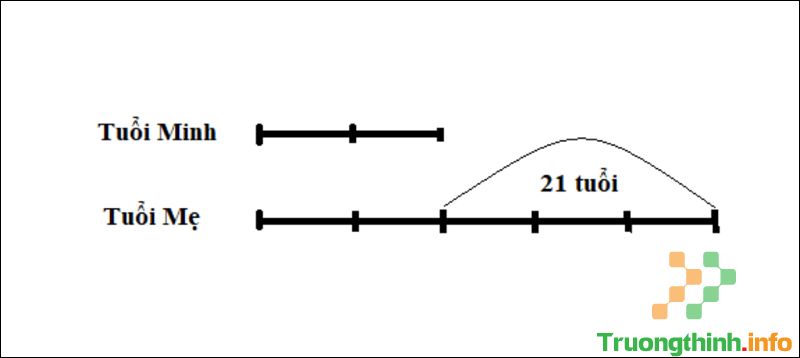
Sơ đồ bài toán

+ Tính hiệu số phần bằng nhau: 5 – 2 = 3 (phần).

+ Tính giá trị của một phần bằng nhau: 21 : 3 = 7 (tuổi).

+ Xác định số bé (tuổi của Minh): 2 x 7 = 14 (tuổi).

+ Xác định số lớn (tuổi của Mẹ): 5 x 7 = 35 (tuổi).

+ Kết luận: Vậy tuổi của Minh là 14 tuổi, tuổi của Mẹ là 35 tuổi.

Dạng 2: Dạng toán hiệu (ẩn) – tỉ

Dạng toán hiệu (ẩn) – tỉ là dạng đề cho thấy tỉ số, ẩn hiệu và yêu cầu tìm hiệu của hai thành phần.

Bài tập tỉ dụ : Một mảnh vườn hình chữ nhật có chiều rộng hơn bề dài 42m. Tính diện tích mảnh vườn đó, hiểu được chiều rộng bằng 7/4 chiều dài.

Cách giải :

+ Vẽ lược đồ bài toán.

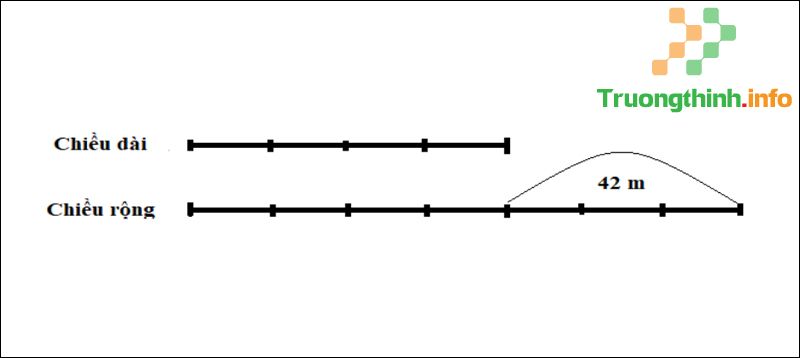
Sơ đò bài toán

+ Tính hiệu số phần bằng nhau: 7 – 4 = 3 (phần).

+ Tính giá trị của 1 phần bằng nhau: 42 : 3 = 14m.

+ Xác định số bé (chiều dài): 14 x 4 = 56m.

+ Xác định số lớn (chiều rộng): 14 x 7 = 98m.

+ Tính diện tích mảnh đất: 56 x 98 = 5488 (m2).

+ Kết luận: Vậy diện tích mảnh đất là 5488 (m2).

Dạng 3: Dạng toán hiệu – tỉ (ẩn)

Dạng toán hiệu – tỉ (ẩn) là dạng đề cho thấy hiệu của hai thành phần, ẩn tỉ và yêu cầu tìm từng thành phần.

Bài tập ví dụ : Có hai thùng dầu, thùng thứ nhất đựng ít hơn thùng thứ 2 24 lít dầu. Biết 5 lần thùng thứ nhất bằng 3 lần thùng thứ hai. Hỏi mỗi thùng đựng bao nhiêu lít dầu?

Cách giải :

+ Xác định tỉ số của thùng thứ nhất so với thùng thứ hai: 3/5.

+ Vẽ sơ đồ bài toán.

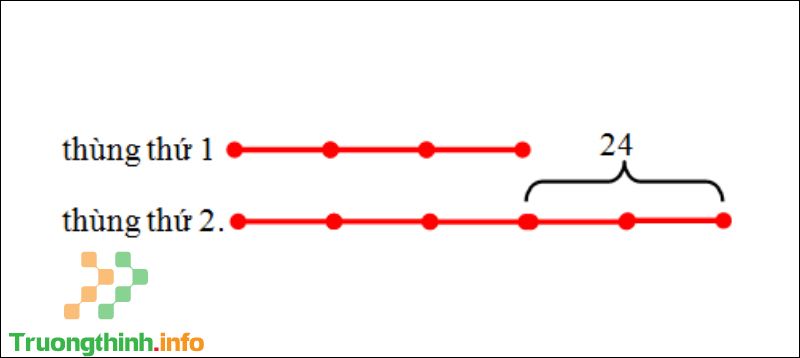
Sơ đồ bài toán

+ Tính hiệu số phần bằng nhau: 5 – 3 = 2 (phần).

+ Xác định số bé (thùng dầu thứ nhất): (24 : 2) x 3 = 36 (lít).

+ Xác định số lớn (thùng dầu thứ hai): 36 + 24 = 60 (lít).

+ Kết luận: Vậy thùng dầu thứ nhất đựng 36 lít dầu, thùng dầu thứ hai đựng 60 lít dầu.

Dạng 4: Dạng toán hiệu (ẩn) – tỉ (ẩn)

Dạng toán hiệu (ẩn) – tỉ (ẩn) là dạng đề cho ẩn cả hiệu lẫn tỉ số và đòi hỏi tìm hiệu và từng phần tử của bài toán.

Bài tập tỉ dụ : Hiện nay, An 8 tuổi và chị Mai 28 tuổi. Sau bao nhiêu năm nữa thì 1/3 tuổi An bằng 1/7 tuổi chị Mai?

Cách giải :

+ Vẽ sơ đồ bài toán.

Sơ đồ bài toán

+ Tính hiệu số tuổi của An và Mai: 28 – 8 = 20 (tuổi).

+ Xác định tỉ số của tuối của An so với tuổi của Mai: 3/7.

+ Tính hiệu số phần bằng nhau: 7 – 3 = 4 (phần).

+ Tính số tuổi của An sau này: (20 : 4) x 3 = 15 (tuổi).

+ Tính số năm cần tìm: 15 – 8 = 7 (năm).

+ Kết luận: Vậy sau 7 năm nữa thì 1/3 tuổi An bằng 1/7 tuổi Mai.

Dạng 5: Dạng ẩn mối liên hệ

Dạng ẩn mối quan hệ là dạng đề cho các dữ kiện liên quan từ đấy tìm hiệu và từng thành phần.

Bài tập thí dụ : Bình và An có hai thửa ruộng, tổng diện tích của hai thửa ruộng đó là 930. Nếu chuyển 1/6 diện tích ruộng của Bình sang cho An thì diện tích của hai thửa sẽ bằng nhau. Tính diện tích của mỗi thửa ruộng bằng mét vuông.

Cách giải :

+ Tính hiệu số phần bằng nhau: 6 – 1 = 5 (phần).

+ Xác định giá trị của 1 phần bằng nhau: 930 : 5 = 116 (m2).

+ Tính diện tích thửa thứ nhất: 116 x 1 = 116 (m2).

+ Tính diện tích thửa thứ hai: 116 x 5 = 580 (m2).

+ Kết luận: Vậy diện tích thửa thứ đặc biệt là 116 m2, diện tích thửa thứ hai là 580 m2.

5. Bài tập về tìm 2 số lúc biết hiệu và tỉ số có lời giải

Bài tập trắc nghiệm

Câu 1 : Hiệu của 2 số là 57. Tỉ của hai số đó là 2/5. Tìm số bé.

A. 38.

B. 48.

C. 28.

D. 18.

Đáp án :

Ta có sơ đồ:

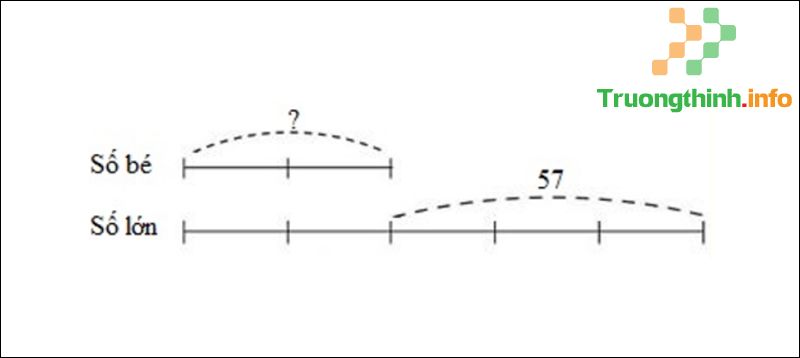
Sơ đồ câu 1

Theo sơ đồ, hiệu số phần bằng nhau là: 5 – 2 = 3 (phần).

Số bé là: 57 : 3 x 2 = 38.

Đáp số: A. 38.

Câu 2 : Một dịch vụ có số gạo tẻ nhiều hơn số gạo nếp là 135kg. Biết số gạo nếp bằng 3/8 số gạo tẻ. Tính số gạo mỗi loại?

A. 212kg gạo tẻ; 77kg gạo nếp.

B. 222kg gạo tẻ; 87kg gạo nếp.

C. 216kg gạo tẻ; 81kg gạo nếp.

D. 225kg gạo tẻ; 90kg gạo nếp.

Đáp án :

Ta có sơ đồ:

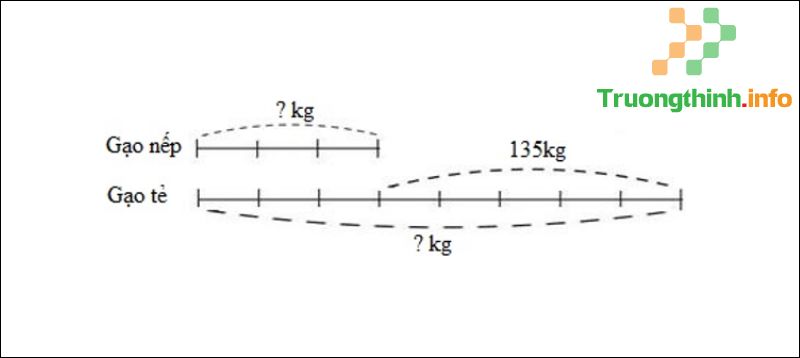
Sơ đồ câu 2

Theo sơ đồ, hiệu số phần bằng nhau là: 8 – 3 = 5 (phần).

Cửa hàng đó có số ki-lô-gam gạo tẻ là: 135 : 5 x 8 = 216 (kg).

Cửa hàng đó có số ki-lô-gam gạo nếp là: 216 – 135 = 81 (kg).

Đáp số: C. 216kg gạo tẻ; 81kg gạo nếp.

Câu 3 : Hiểu của hai số chẵn thật lớn có ba chữ số. Biết số lớn gấp 3 lần số bé. Tìm số lớn.

A. 1479.

B. 1489.

C. 1497.

D. 1498.

Đáp án :

Số chẵn lớn số 1 có ba chữ số là 998. Vậy hiệu của hai số là 998.

Ta có sơ đồ:

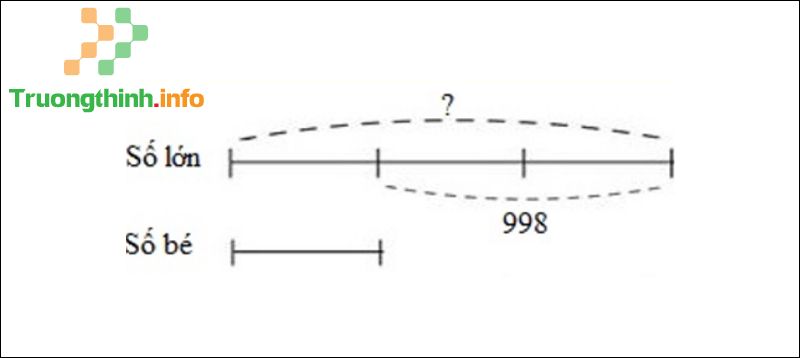
Sơ đồ câu 3

Theo sơ đồ, hiệu số phần bằng nhau là: 3 – 1 = 2 (phần).

Số lớn là: 998 : 2 x 3 = 1497.

Đáp số: C. 1497.

Câu 4 : Giải toán theo lược đồ sau:

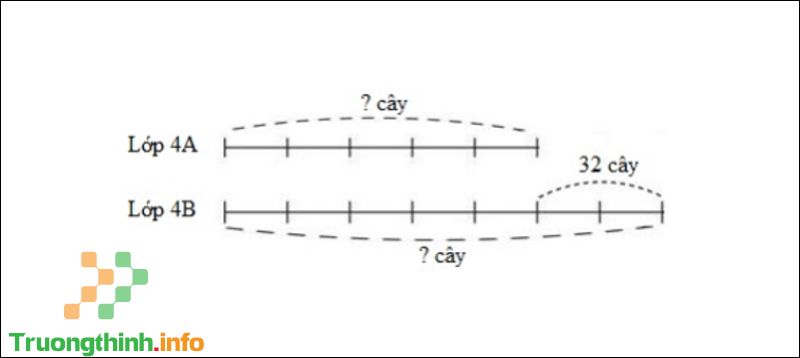
Sơ đồ câu 4

A. Lớp 4A: 90 cây; lớp 4B: 122 cây.

B. Lớp 4A: 75 cây; lớp 4B: 107 cây.

C. Lớp 4A: 85 cây; lớp 4B: 117 cây.

D. Lớp 4A: 80 cây; lớp 4B: 112 cây.

Đáp án :

Theo sơ đồ, hiệu phân số bằng nhau là: 7 – 5 = 2 (phần).

Lớp 4A trồng được số cây là: 32 : 2 x 5 = 80 (cây).

Lớp 4B trồng được số cây là: 80 + 32 = 112 (cây).

Đáp số: D. Lớp 4A: 80 cây; lớp 4B: 112 cây.

Câu 5 : Tỉ số của số thứ nhất và số thứ hai là 9/7 thì khi vẽ sơ đồ ta vẽ:

A. Số thứ nhất là 7 phần, số thứ 2 là 9 phần,

B. Số thứ nhất là 9 phần, số thứ 2 là 7 phần.

C. Số thứ đặc biệt là 7 phần, số thứ hai là 16 phần.

D. Số thứ nhất là 9 phần, số thứ 2 là 16 phần.

Đáp án : B.

Tỉ số của số thứ nhất và số thứ 2 là 9/7 có tức là số thứ nhất bằng 9/7 số thứ hai. Vậy nếu coi số thứ 2 là 7 phần thì số thứ nhất là 9 phần như thế.

Câu 6 : Điền số thích hợp vào chỗ trống (…).

Hiểu của 2 số là 57. Tỉ số của hai số đó là 2/5.

Vậy số bé là …

A. 45.

B. 38.

C. 47.

D. 39.

Đáp án : B.

Ta có sơ đồ:

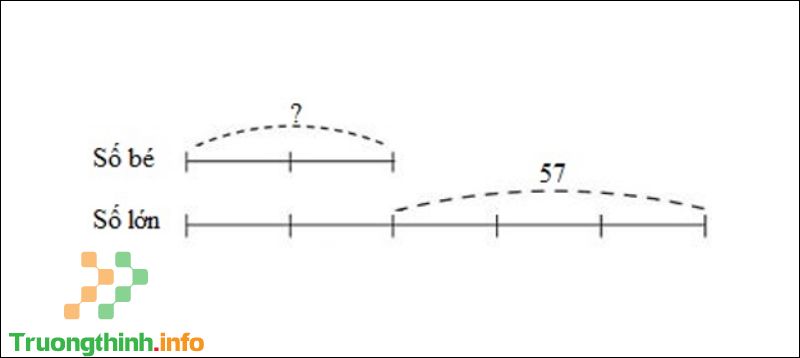
Sơ đồ câu 6

Theo sơ đồ, hiệu số phần bằng nhau là: 5 – 2 = 3 (phần).

Số bé là: 57 : 3 x 2 = 38.

Câu 7 : Điền số thích hợp vào chỗ trống (…).

Hiệu của hai số là 224, nếu giảm số lớn đi 5 lần thì ta được số bé. Vậy tổng của hai số đó là …

A. 335.

B. 337.

C. 334.

D. 336.

Đáp án : D.

Theo đề giảm số lớn đi 5 lần thì ta được số bé nên tỉ số của số bé và số lớn là 1/5.

Ta có sơ đồ:

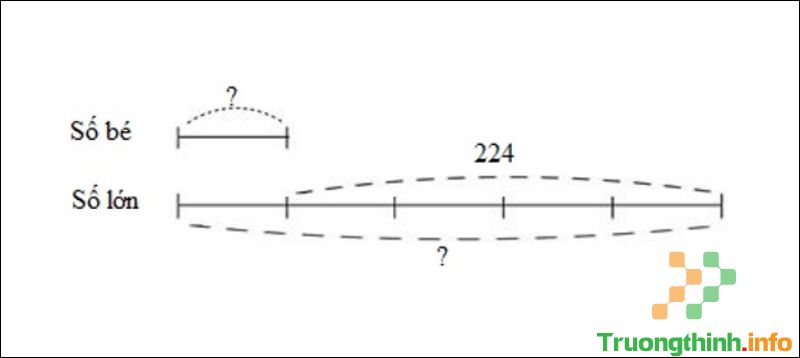
Sơ đồ câu 7

Theo sơ đồ, hiệu số phần bằng nhau là: 5 – 1 = 4 (phần).

Số lớn là: 224 : 4 x 5 = 280.

Số bé là: 280 – 224 = 56.

Tổng hai số đó là: 280 + 56 = 336.

Câu 8 : Hiện nay mẹ hơn con 25 tuổi. Cách đây 5 năm tuổi mẹ gấp 6 lần tuổi con. Tính tuổi của mỗi người hiện nay.

A. Con 5 tuổi, mẹ 30 tuổi.

B. Con 7 tuổi, mẹ 32 tuổi.

C. Con 10 tuổi, mẹ 35 tuổi.

D. Con 9 tuổi, mẹ 39 tuổi.

Đáp án : C.

Vì mỗi năm mỗi người tăng thêm 1 tuổi nên hiệu số tuổi không thay đổi. Do đó, cách đây 5 năm mẹ vẫn hơn con 25 tuổi.

Ta có lược đồ tuổi của hai mẹ con cách đây 5 năm:

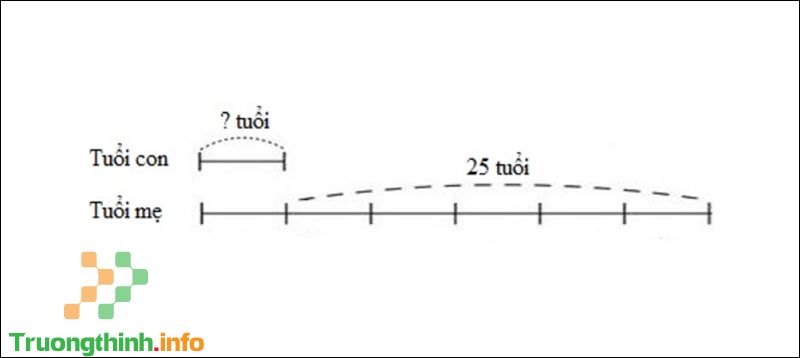
Sơ đồ câu 8

Theo sơ đồ, hiệu số phần bằng nhau là: 6 – 1 = 5 (phần).

Tuổi con cách đây 5 năm là: 25 : 5 x 1 = 5 (tuổi).

Tuổi con hiện nay là: 5 + 5 = 10 (tuổi).

Tuổi mẹ hiện giờ là: 10 + 25 = 35 (tuổi).

Câu 9 : Một hình thoi có tính dài đường chéo lớn hơn độ dài đường chéo bé là 51cm. Tính diện tích hình thoi đó, biết rằng tỉ số giữa độ dài đường chéo lớn và độ dài đường chéo bé là 7/4.

A. 4046cm2.

B. 4064cm2.

C. 8092cm2.

D. 8128cm2.

Đáp án : A.

Ta có sơ đồ:

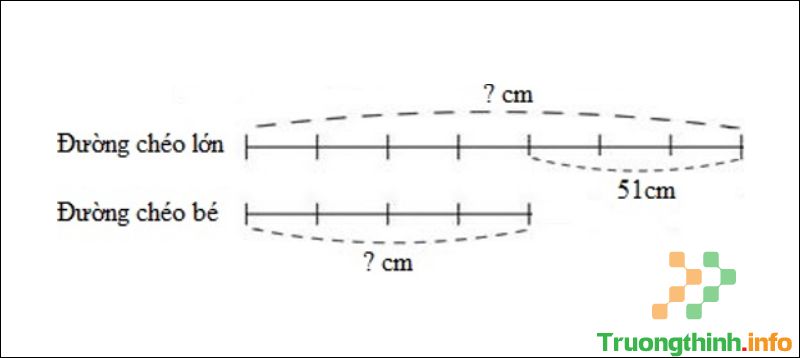
Sơ đồ câu 9

Theo sơ đồ, hiệu số phần bằng nhau là: 7 – 4 = 2 (phần).

Độ dài đường chéo lớn là: 51: 3 x 7 = 119 (cm).

Độ dài đường chéo bé là: 119 – 51 = 68 (cm).

Diện tích hình thoi đó là: 119 x 68 : 2 = 4046 (cm2).

Câu 10 : Hiệu của hai số là 156. Tỉ số của hai số đó là 5/7. Vậy hai số đó là:

A. 395; 541.

B. 390; 546.

C. 385; 551.

D. 380; 556.

Đáp án : B.

Ta có sơ đồ:

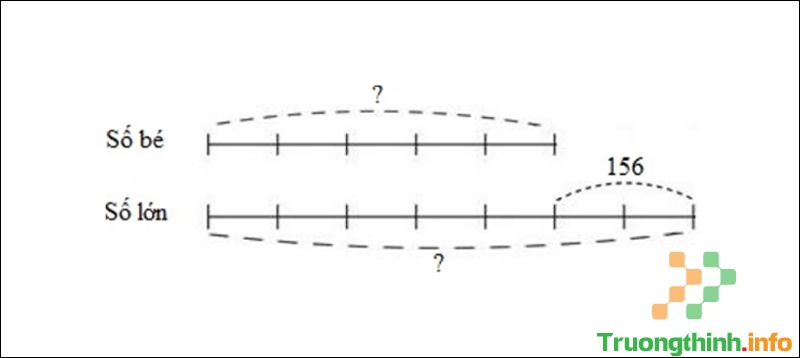
Sơ đồ câu 10

Theo sơ đồ, hiệu số phần bằng nhau là: 7 – 5 = 2 (phần).

Số bé là: 156 : 2 x 5 = 390.

Số lớn là: 390 + 156 = 546.

Bài tập tự luận

Câu 1 : An có nhiều hơn Bình 18 quyển vở. Tìm số vở của mỗi bạn biết rằng, số vở của An gấp 4 lần số vở của Bình.

Đáp án :

Ta có sơ đồ:

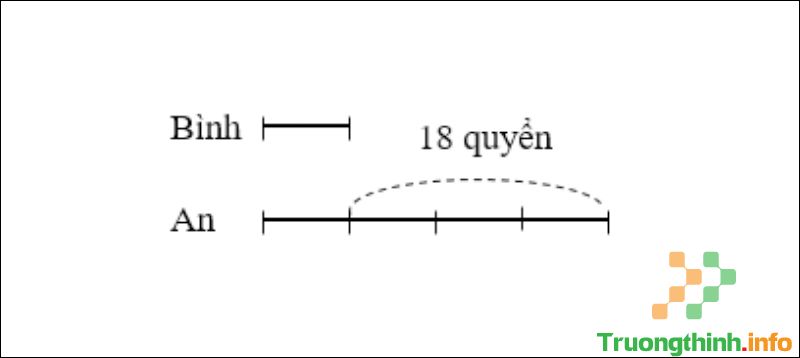
Sơ đồ

Hiệu số phần bằng nhau là: 4 – 1 = 3 (phần).

Số vở của Bình là: 18 : 3 x 1 = 6 (quyển).

Số vở của An là: 18 + 6 = 24 (quyển).

Đáp số: Bình 6 quyển vở; An 24 quyển vở.

Câu 2 : Số thứ nhất bằng 2/5 số thứ hai. Tìm hai số biết rằng nếu viết thêm nữa số thứ nhất 120 công ty và bớt đi số thứ hai 243 dịch vụ thì hai số bằng nhau.

Đáp án :

Hiệu hai số đó là: 120 + 243 = 363.

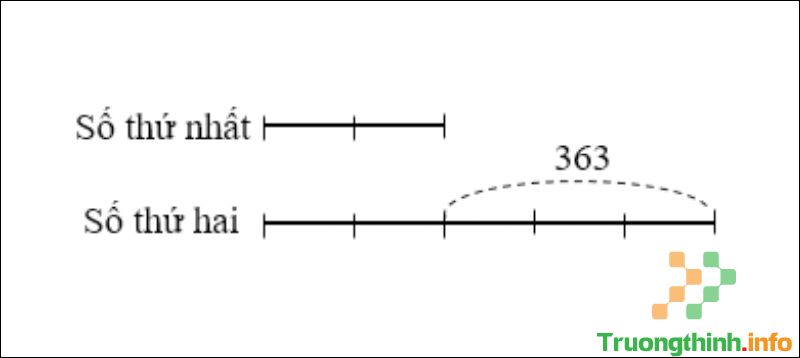
Sơ đồ

Hiệu số phần bằng nhau là: 5 – 2 = 3 (phần).

Số thứ nhất là: 363 : 3 x 2 = 242.

Số thứ hai là: 242 + 363 = 605.

Đáp số: Số thứ nhất: 242; Số thứ hai: 605.

Câu 3 : Năm nay 1/7 tuổi bố bằng 1/2 tuổi con. Biết rằng bố hơn con 30 tuổi.Hỏi năm nay bố bao nhiêu tuổi?

Đáp án :

Ta có sơ đồ:

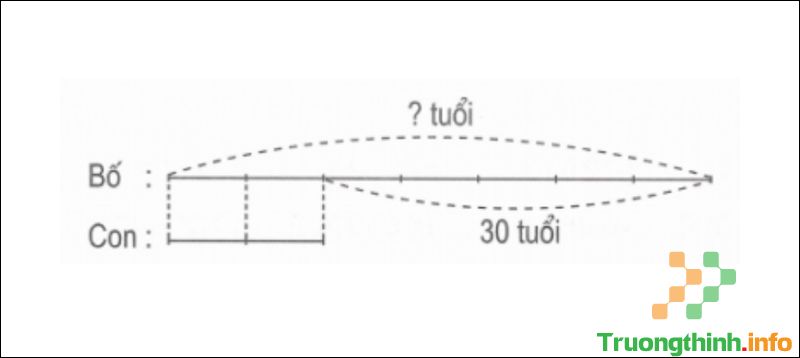
Sơ đồ

Theo sơ đồ, hiệu số phần bằng nhau là: 7 – 2 = 5 (phần).

Tuổi bố năm nay là: 30 : 5 x 7 = 42 (tuổi).

Đáp số: Tuổi bố năm nay là 42 tuổi.

Câu 4 : Tìm hai số có hiệu bằng 165, biết rằng nếu lấy số lớn chia cho số bé thì được thương là 7 và có số dư là 3.

Đáp án :

Ta có sơ đồ:

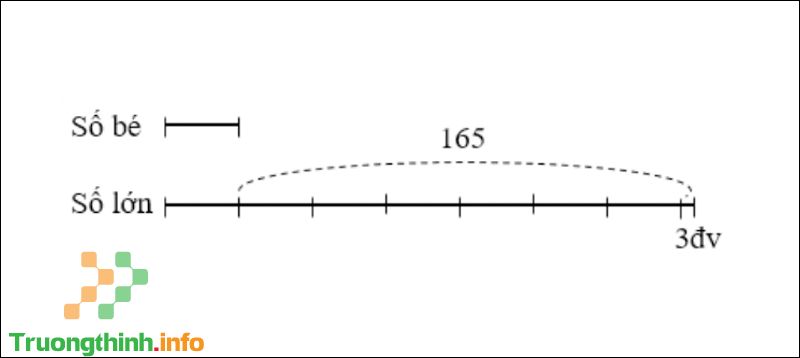
Sơ đồ

Hiệu số phần bằng nhau là: 7 – 1 = 6 (phần).

Số bé là: (165 – 3) : 6 x 1 = 27.

Số lớn là 165 + 27 = 192.

Đáp số: Số lớn: 192; Số bé: 27.

Câu 5 : Hiện nay An 8 tuổi và chị Mai 28 tuổi. Sau bao nhiêu năm nữa thì 1/3 tuổi An bằng 1/7 tuổi chị Mai?

Đáp án :

Chị Mai lớn hơn An số tuổi là: 28 – 8 = 20 (tuổi).

Số tuổi của An bằng số phần tuổi của chị Mai là: 1/3 : 1/7 = 3/7.

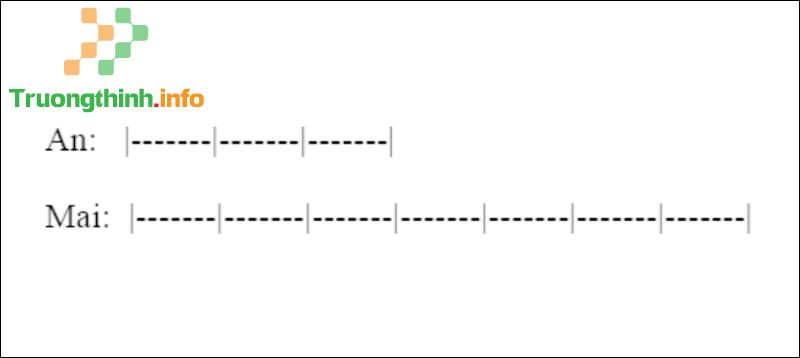
Sơ đồ

Hiệu số phần bằng nhau là: 7 – 3 = 4 (phần).

Số tuổi của An lúc đấy là: 20 : 4 x 3 = 15 (tuổi).

Số năm để 1/3 tuổi An bằng 1/7 tuổi chị Mai là: 15 – 8 = 7 (năm)

Đáp số: 7 năm.

Câu 6 : Hiệu của hai số là 36. Tỉ số của hai số đó là 8/5. Tìm hai số đó.

Đáp án :

Ta có sơ đồ:

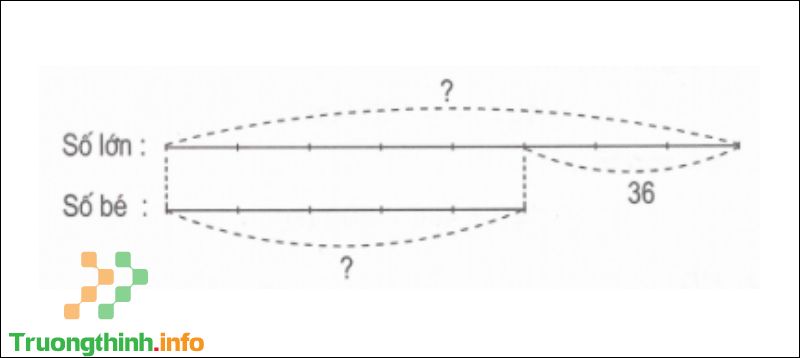
Sơ đồ

Theo sơ đồ, hiệu số phần bằng nhau là: 8 – 5 = 3 (phần).

Số bé là: 36 : 3 x 5 = 60.

Số lớn là: 60 + 36 = 96.

Đáp số: Số bé: 60; Số lớn: 96.

Câu 7 : Bố cao hơn con 68. Tỉ số giữa độ cao của bố và chiều cao của con là 5 : 3. Tính độ cao của bố.

Đáp án :

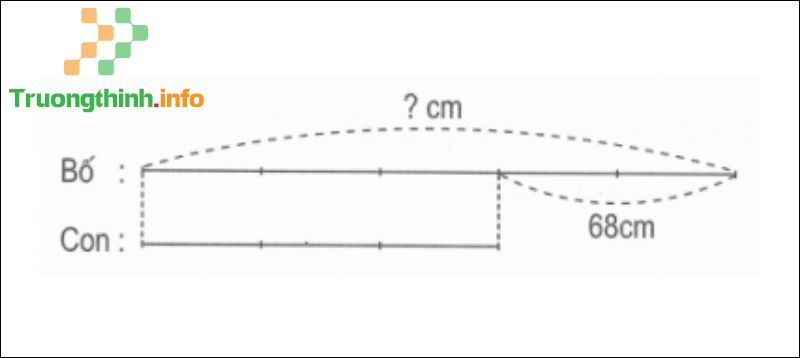
Sơ đồ

Theo sơ đồ, hiệu số phần bằng nhau là: 5 – 3 = 2 (phần).

Chiều cao của bố là: 68 : 2 x 5 = 170 (cm).

Câu 8 : Một trường tiểu học có số học trò nữ ít hơn số học trò nam là 120 học sinh. Hỏi trường đó có bao nhiêu học sinh nam, biết rằng số học trò nữ bằng 5/7 số học sinh nam?

Đáp án :

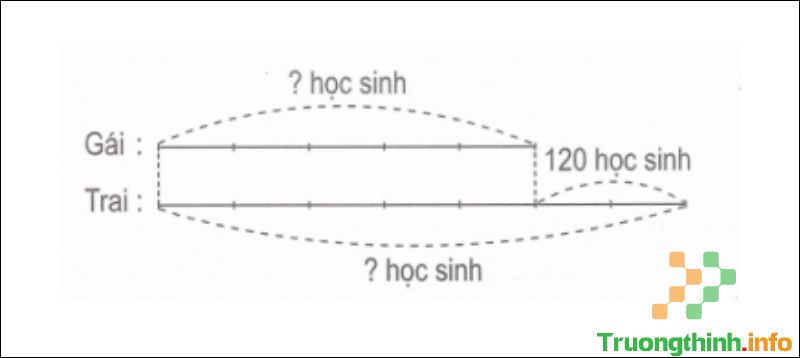
Sơ đồ

Theo sơ đồ, hiệu số phần bằng nhau là: 7 – 5 = 2 (phần).

Số học trò gái là: 120 : 2 x 5 = 300 (học sinh).

Số học sinh trai là: 300 + 120 = 420 (học sinh).

Câu 9 : Một mảnh vườn hình chữ nhật có bề dài hơn bề rộng 15m. Tính diện tích mảnh vườn đó, hiểu được bề rộng bằng 3/4 chiều dài.

Đáp án :

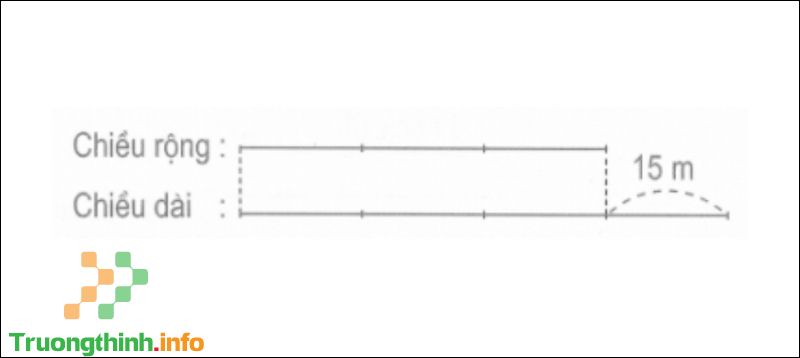
Sơ đồ

Chiều rộng mảnh vườn là: 15 x 3 = 45 (m).

Chiều dài mảnh vườn là: 15 x 4 = 60 (m).

Diện tích mảnh vườn đó là: 60 x 45 = 2700 (m2).

Câu 10 : Hiệu của hai số ngay số lớn nhất có hai chữ số. Tỉ số của hai số đó là 20. Tìm hai số đó.

Đáp án : Số lớn số 1 có hai chữ số là 99 nên hiệu của 2 số đó là 99.

Hiệu số phần bằng nhau là: 20 – 9 = 11 (phần).

Số bé là: 99 : 11 x 9 = 81.

Số lớn là: 81 + 99 = 180.

6. Bài tập tự luyện về tìm 2 số khi biết hiệu và tỉ

Câu 1 : Tìm hai số biết tỉ số của chúng bằng 4/7 và nếu lấy số lớn trừ đi số bé thì được kết quả bằng 360.

Câu 2 : An có nhiều hơn Bình 12 quyển vở. Tìm số vở của mỗi bạn. Biết rằng số vở của An gấp 4 lần số vở của Bình.

Câu 3 : Hiện nay mẹ hơn con 28 tuổi. Biết rằng 3 năm tiếp theo tuổi của con bằng 3/7 tuổi mẹ. Hỏi hiện nay mỗi người bao nhiêu tuổi?

Câu 4 : Tìm hai số có tỉ số là 1/9, biết rằng số lớn là số có ba chữ số và nếu xóa chữ số 4 ở hàng trăm của số lớn thì được số bé.

Câu 5 : Số thứ nhất bằng 2/5 số thứ hai. Tìm hai số đó? Biết rằng nếu viết thêm nữa số thứ nhất 120 trung tâm và bớt 243 dịch vụ thì hai số bằng nhau.

Câu 6 : Mảnh đất hình chữ nhật có bề rộng bằng 3/5 chiều dài. Biết rằng nếu giảm chiều dài 9m và tăng chiểu rộng thêm 7m thì mảnh đất có dạng hình vuông. Tính diện tích mảnh đất hình chữ nhật đó?

Câu 7 : Lớp 4A có 1/3 số học trò nam bằng 1/5 số học sinh nữ. Biết rằng số học sinh nữ hơn số học trò nam là 10 bạn. Tìm số học trò nam, số học trò nữ.

Câu 8 : Tìm hai số có hiệu bằng 216, biết rằng nếu thêm một chữ số 0 vào bên phải số bé thì nó lớn.

Câu 9 : Hiệu của hai số bằng 393, hiểu được nếu xóa chữ số cuối của số lớn thì được số bé.

Câu 10 : Hiện nay bố 32 tuổi, em 5 tuổi. Hỏi bao nhiêu năm nữa tuổi của bố gấp 5 lần tuổi của con.

Câu 11 : Mẹ sinh con khi 24 tuổi. Biết hiện nay tuổi mẹ gấp 4 lần tuổi con. Tính tuổi mẹ sau hai năm nữa.

Câu 12 : Viết thêm chữ số 8 vào bên phải số tự nhiên có 3 chữ số thì số đó tăng 2312 đơn vị. Tìm số có 3 chữ số đó.

7. Một số lỗi sai thường mắc phải khi làm bài tìm số khi biết hiệu và tỉ số

Bài toán tìm hai số khi biết hiệu và tỉ là một loại bài không hơn phức tạp trong cách giải. Tuy nhiên khi gặp những dạng đề ẩn, các bạn học sinh rất dễ mắc những lỗi sau:

+ Hiểu sai bản chất bài toán.

+ Gộp bước làm, làm tắt nên tính toán sai.

+ Quên ghi đơn vị.

Một số lỗi sai thường gặp phải

8. Một số lưu ý giúp bạn học tốt về dạng toán tìm 2 số lúc biết hiệu và tỉ

– Làm bài tập đều đặn để rèn dũa khả năng và vận tốc giải bài tập.

– Hiểu rõ các mối quan hệ giữa hiệu và tỉ.

– Phân biệt được những dạng bài tập để tạo nên cách áp dụng đúng.

Một số lưu ý giúp học tốt

– Thuộc một số công thức hình học cơ bản.

– Sử dụng máy tính cầm tay khi làm bài tập để tạo nên kết quả nhanh và đúng nhất.

Một số mẫu Máy tính cầm tay Flexio đang mua bán tại Chúng tôi:

Trên này là bài viết tổng hợp lý thuyết tìm hai số khi biết hiệu và tỉ hai số đó. Rất mong bài viết sẽ hữu ích với bạn và hẹn tái ngộ ở những bài viết sau!

tìm hai số khi biết hiệu và tỉ hai số đó,hiệu và tỉ,toán lớp 4,bài tập tìm hai số khi biết hiệu và tỉ

Nội dung ✔️ Lý thuyết và bài tập tìm hai số khi biết hiệu và tỉ của hai số đó – Tin Công Nghệ được tổng hợp sưu tầm biên tập bởi 1️⃣❤️: Trường Thịnh Group. Mọi ý kiến vui lòng gửi Liên Hệ cho truongthinh.info để điều chỉnh. truongthinh.info tks.